최대 유량 문제 (Maximum Flow)
최대 유량 문제(Maximum Flow)란 방향 그래프에서 각 간선의 용량이 정해져 있을 때, 정해진 출발점에서 도착점까지 보낼 수 있는 최대의 유량을 계산하는 문제를 말한다.

위와 같이 생긴 방향 그래프의 1번 정점에서 7번 정점까지의 최대 유량인 상황은 아래 그림과 같다.
간선에 적힌 a/b는 용량이 b인 간선에 현재 a의 유량이 흐르고 있다는 것을 말한다.

이 경우의 유량은 11이다. 더 이상의 유량이 없다는 것은 어떻게 알 수 있을까?
최소 1의 유량이 흐를 수 있는 출발점에서 도착점까지 가는 경로를 증가경로(Augmented Path)라고 한다.
위 그래프에서 증가경로는 없다는 사실을 눈으로도 쉽게 확인할 수 있으며,
임의의 그래프에 대해서도 DFS/BFS를 이용하여 어렵지 않게 구할 수 있다.
(화제가 된지 얼마 되지 않아서 최대 유량 문제를 푸는 가장 빠른 알고리즘은 지금도 계속해서 갱신되고 있다고 한다.) PS에서는 주로 최대 유량 문제를 O(VE^2)에 처리하는 에드몬드-카프 알고리즘(Edmonds-Karp Algorithm)을 가장 많이 사용한다. 에드몬드-카프 알고리즘을 설명하기 전, 이를 포함하는 개념인 포드-풀커슨 알고리즘(Ford-Fulkerson Algorithm)에 대해 먼저 설명하겠다.
포드-풀커슨 알고리즘 (Ford-Fulkerson Algorithm)
때에 따라 포드-풀커슨 방법이라고 부르기도 한다. 알고리즘이라고 하기에는 구현에 따라 시간복잡도가 달라지기도 하며, 정확한 단계보다는 최대 유량 문제를 해결하는 큰 틀을 제시하기 때문이다.
포드-풀커슨 알고리즘은 증가경로가 나오지 않을 때까지 유량을 그리디하게 흘려주는 방식이다.
과연 그리디가 통할까? (대충 통하니까 알고리즘이 있겠지)

초기 그래프에서 DFS를 적용하여 증가경로인 1-2-4-7를 찾았다고 하자.
간선 1-2는 3 / 간선 2-4는 5 / 간선 4-7은 7의 용량을 가지고 있으므로, 이 증가 경로에는 최대 3의 유량이 흐를 수 있다.
따라서 그리디하게 유량 3을 흘려준 그림이 위와 같다.

간선 1-2의 유량이 용량에 도달했으므로 증가 경로는 더 이상 간선 1-2를 포함할 수 없다.
따라서 간선 1-3을 사용하는 증가 경로인 1-3-6-7을 찾았고, 흐를 수 있는 최대 유량인 4를 흘려준 그림이 위와 같다.

간선 1-3을 포함하는 증가 경로를 더 이상 찾을 수 없으므로 간선 1-4를 포함하는 증가 경로를 찾는다.
1-4-7을 찾았고, 4-7에 이미 유량 3이 흐르고 있으므로 최대 1까지만 더 흘려줄 수 있다.
현재 유량은 8이며, 위에서 보았듯 최대 유량은 11이었다.
자, 이제 증가경로가 보이지 않는다.
???? (그리디 된다며)
사실 증가경로는 존재한다! 우리 눈에 보이지 않을 뿐이다!
만약 사람에게 이 과제가 주어진다면, 우리는 마지막 그림에서 유량을 어떻게 바꾸었을까?
아마 1-2-4-7에 흐르는 유량을 우회하고, 여유가 생겨 다시 증가 경로가 된 1-4-7의 유량을 늘렸을 것이다.
우리는 이러한 판단을 컴퓨터가 할 수 있도록 만들어야한다.
이 과정은 생각해내기 어려운 하나의 아이디어로 간단하게 해결할 수 있다.
바로, 기존의 간선과 반대 방향인 용량이 0인 간선을 추가한다.
만약 기존의 간선에 유량 n이 흐르고 있었다면, 반대 방향의 간선으로는 유량 -n이 흐른다고 판단한다.
이렇게 되면 반대 방향의 간선에 n만큼의 여유 용량이 생기므로, 해당 간선에 유량을 흘려줄 수 있다.
즉, "반대 방향의 간선에 유량이 흐른다"="기존 간선에 있던 유량을 취소하고 우회한다"이므로, 반대 방향의 간선을 설정해줌으로써 모든 것이 해결된다. 기존의 그리디 코드를 고칠 필요도 없이, 아이디어 하나만으로 그리디 알고리즘을 완성시키는 이 부분이 포드-풀커슨 알고리즘의 가장 중요하면서도 아름다운 부분이다.
포드-풀커슨 알고리즘의 시간복잡도는 얼마나 될까? 다음과 같은 그래프를 생각해보자.
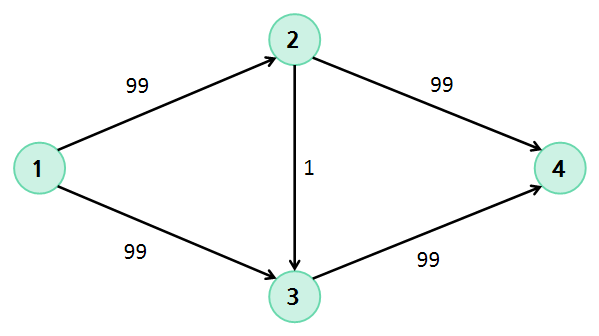
DFS로 경로를 찾는다면 증가경로 1-2-3-4를 가장 먼저 찾을 것이다. 여기에 유량 1을 흘려준다.
그 다음 찾는 경로는 1-3-2-4이다. 간선 3-2의 용량은 0이고, 유량은 -1이므로 최대 1의 유량을 흘려줄 수 있다.
이 두 번의 시행 후의 그래프의 상태는 아래와 같다.

이 방법대로 계속한다면 최대 유량인 99+99=198번의 시행 후에야 최대 유량을 찾을 수 있다.
따라서 DFS로 증가 경로를 찾으면 시간복잡도는 O(Ef)가 된다. (E는 간선의 개수, f는 최대 유량)
만약 저 그래프 간선의 용량이 99가 아니라 999999999였다면 아마 시간 내에 문제를 풀지 못할 것이다.
해결책은 간단하다. DFS만 BFS로 바꾸면 된다.
BFS로 증가 경로를 찾으면 시간복잡도가 O(VE^2)까지 단축된다.
이 경우를 우리는 에드몬드-카프 알고리즘이라고 부른다.
에드몬드-카프 알고리즘 (Edmonds-Karp Algorithm)
증가 경로를 BFS로 찾은 후, 해당 경로에 흐를 수 있는 최대 유량을 흘려준다.
아래는 에드몬드-카프 알고리즘을 시행하는 코드이다.
S는 출발점, E는 도착점, C[i][j]는 간선 ij의 용량, F[i][j]는 간선 ij에 현재 흐르고 있는 유량을 나타낸다.
D[i]는 i와 인접한 정점을 의미하며, pre[i]는 현재 탐색 중인 증가 경로에서 이전 정점을 저장하여 경로를 기억하는 역할을 한다.
while(1) { // 증가 경로가 없을 때까지 반복
queue<int> Q;
memset(pre, -1, sizeof(pre));
Q.push(S);
while (!Q.empty()) {
curr=Q.front();
Q.pop();
for (int next : D[curr]) if (F[curr][next]<C[curr][next] && pre[next]==-1) {
pre[next]=curr; // 경로에서 이전 정점을 저장
Q.push(next);
if (next==E) break; // 증가 경로를 찾음
}
}
if (pre[E]==-1) break; // 증가 경로가 없음
int flow=1e9;
for (int i=E; i!=S; i=pre[i]) flow=min(flow, C[pre[i]][i]-F[pre[i]][i]);
for (int i=E; i!=S; i=pre[i]) {
F[pre[i]][i]+=flow;
F[i][pre[i]]-=flow;
}
ans+=flow;
}
cout << ans;
에드몬드-카프 알고리즘 문제 해결 순서
① 문제에 맞게 방향 그래프를 설정한다. 양방향 간선이면 양쪽 유량을 모두 설정해준다.
이때, 방향 간선이더라도 반대 방향도 연결해주어야 한다는 사실을 잊으면 안된다. (용량이 0인 간선)
② BFS로 증가 경로를 찾고, 해당 경로에 추가로 흘릴 수 있는 최대 유량을 계산하여 더한다.
③ 증가 경로를 더 이상 찾을 수 없을 때까지 ②를 반복한다.
최대 유량 연습 문제
최대 유량 [BOJ 6086] (P4)
에드몬드-카프 알고리즘을 사용하는 가장 기본적인 문제, 양방향 간선이 특징
문제 링크 : https://www.acmicpc.net/problem/6086
풀이 링크 : 추후 포스팅 예정 (쉬워서 안 할 수도?)
책 구매하기 2 [BOJ 11406] (P4)
출발점, 도착점 및 방향 그래프를 직접 만들어야하는 문제
이 형태의 그래프는 이분매칭 등에서 많이 만들 것이기 때문에 풀어보는 것 추천!
문제 링크 : https://www.acmicpc.net/problem/11406
풀이 링크 : 추후 포스팅 예정