총점 : 1교시 139 + 2교시 213 = 352 (가채점 결과 3.467%, 77등, 은상)
<세 줄 요약>
1. 1교시가 어려웠다.
2. 2교시가 많이 망한줄 알았으나 생각만큼 망한건 아니었다.
3. 2교시 3번은 Dumae와 거의 같은 문제이다.
작년에 플5짜리 문자열 문제를 못 풀고 1차 탑골드를 놓쳐 많이 아쉬웠다. 비버챌린지는 196.xx점이어서 실수한 소문제 2개에서만 감점이 있었기에, 이번에도 2교시가 지난 해와 비슷한 난이도로 나오면 만점에 가까운 점수로 탑골드를 노릴 수 있다고 생각하고 시험에 들어갔다.
1교시. 비버챌린지형(200점) - 킬러 문제 및 배점이 큰 문제에는 굵은 글씨를 해두었다.
총평 - 단답형 12번이 어려웠고, 시뮬레이션형 문제 17, 19, 20번 난이도가 작년 기준 가장 어려운 문제의 난이도 정도였던 것 같다. 즉, 킬러 문제의 개수에 따라 시간이 부족했고, 내 점수도 50점 이상 떨어졌다. 평균도 많이 떨어질 것 같다.
1. 달리기
CDAEB 또는 DCAEB만 가능하여 A가 항상 3등이다.
2. 거스름돈
7원 9원 11원 세 가지 종류의 동전으로 x원 이상의 정수인 금액을 모두 만들 수 있을 때, 최소의 x
잘 노가다 해보면 x=27
3. 블록 쌓기
블록을 쌓는데, 쌓는 맞닿는 면 중에 밑에 있는 면이 위에 있는 면을 완전히 포함해야한다.
(2,5,8), (4,4,9), (3,2,4)를 가장 높이 쌓는 문제인데, 가장 큰 9를 버리고 8+4+4=16을 해버리면 최대이다.
4. 점 잇기
원주 상의 8개의 점을 선분이 교차하지 않도록 4개의 선분으로 짝짓는 경우의 수를 구하는 문제이다.
카탈란 수 문제인 것을 알고 있었고, C4=14라는 것을 알고 있어서 바로 고르고 넘어갔다.
5. 구슬 뽑기 -7점
조건부 확률 문제이다. P(A교B)/P(A)를 해주었어야 하는데 P(A)를 구해놓고도 나누는 것을 까먹어서 틀렸다. 그래서 원래 답은 2/3인데 1/3을 답으로 제출해버렸다.
여기서 -7점
6. 막대기 세우기
Bad Hair Day의 조건을 만족하는 배치를 찾으면 되는데, 6이 각각 3번째, 4번째, 5번째 위치에 있을 때 경우의 수를 구하여 더해주면 105가지가 된다.
7. 세 수의 곱
12개의 정수로 이루어진 수열에서 서로 다른 세 수를 곱하여 그 곱이 최대가 되도록 하는 문제이다. 절댓값이 가장 큰 걸 다 곱해버리면 운 좋게 양수가 되어서 쓰면 된다. 답은 (-6)*6*(-7)=252
8. 2310
서로 다른 세 양의 정수 a<b<c에 대해 abc=2310인 a, b, c의 순서쌍을 구하는 것이다. 2310=2*3*5*7*11이어서 답은 (3^5-3)/(3!)=40이다. 빼기 3을 해준 이유는 a, b, c 중 2개가 1이 되는 경우가 3번 있기 때문이다.
9. 초콜릿
14칸짜리 초콜릿이 있는데 중간에 결함이 있는 칸이 4칸 있다. 초콜릿은 2개 또는 3개로 잘라서 판매할 수 있는데, 결함이 있는 초콜릿과 없는 초콜릿은 가격이 다르다. 해당 초콜릿을 팔아서 얻을 수 있는 최대 금액을 묻는 문제이다.
단순 손DP이다. 8번째 칸까지는 대충 아무렇게나 잘라도 금액이 똑같고, 말짱한 초콜릿 3개인 9, 10, 11을 하나로 묶어 판매하는 것이 중요한 부분이다. 답은 25이다.
10. 순열 거듭제곱
대충 순열 사이클 분할을 하여 주기를 구해주면 된다. 순열 사이클이 총 4개가 묶이고, 이에 따라 m에 대한 정보를 얻을 수 있다. 내가 얻은 정보는 m=1(mod 2), m=0(mod 3), m=3(mod 4), m=1(mod 5)였고 이를 연립하면 m=51(mod 60)이 나온다. 따라서 m의 최솟값은 51이다.
11. 동전 게임
7의 배수 칸은 동전을 놓을 수 없으며, 0번 칸에 놓인 동전을 1, 2, 3칸을 영희와 철수가 번갈아 옮겨 k번째 칸에 도착하면 승리한다. k=22, k=24, k=32일때 필승 전략이 있는 사람을 묻는 문제이다.
이 문제 역시 초콜릿과 같이 손DP이다. 게임이론 문제를 많이 풀어본 사람이라면 나와 똑같이 접근했을 것 같다. dp[k]를 k번째 칸에 도착하면 승리하는 게임에서 필승 전략을 가지고 있는 사람이라고 할 때, 일반적인 경우 dp[k]=dp[k-4]이다. 하지만 k-4번째 칸이 7의 배수인 경우 dp[k]=dp[k-5]가 된다. 초항 몇 개 구하고 이 식을 가지고 모든 32번째 dp값까지 빠르게 구할 수 있다. (그런데 나는 중간에 뇌절을 해서 빠르게,,, 는 못 구했다.) 답은 영희, 철수, 영희이다.
12. 아이템 배치(15점) -15점
단답형 마지막 문제인만큼 어려웠다.

이렇게 생긴 7*8 격자의 빈칸 46개에 ITEM을 적절히 설치하여, 시작->끝으로 가는 모든 최단 경로에 ITEM이 정확히 1개만 되도록하는 경우의 수를 구하는 문제이다. X표시가 되어있는 구간은 방문할 수 없다.
대충 x행 y열이라고 부르면 x+y가 같은 곳끼리만 생각해주면 되고, 테트리스 S자 블록과 Z자 블록으로 막혀있는 부분만 따로 고려해주면 된다. 그리고 5행 2열과 6행 4열은 절대 방문할 수 없는 곳이므로, ITEM의 여부가 중요하지 않다. 따라서 마지막 구한 답에 *4를 해주어야한다. 나는 대충 이 풀이와 비슷한 것을 떠올리긴 했으나 시간이 오래걸릴 것 같아 나중으로 미루었고, 결국 풀지 못해 784라고 찍었다. 답은 888이다. 풀려고 노력했으면 풀 수는 있었겠으나, 시간이 좀 오래걸렸을 것 같다.
여기서 -15점
13. 한붓 그리기

한붓 그리기의 가능 조건은 차수가 홀수인 정점이 2개 또는 0개라는 사실은 잘 알려져있다. 여기서는 간선 3개를 적절히 그어 차수가 홀수인 정점을 0개로 만들어줄 수 있다.
14. 수열 만들기
0으로 초기화된 수열과 타깃 수열이 있을 때, 원하는 구간에 원하는 수를 더하는 것을 반복하여 타깃 수열을 만드는 것이 목표이다. 이때, 더하는 행위를 최소화해야한다. 답은 10회로, 생각보다 너무 많아서 좀 고민했지만 더 이상 줄일 수 없을 것 같아 그냥 넘겼다. [3, 5, 2] 같은 것이 있었다면 많은 사람이 틀렸을 것 같다.
15. 트리 순회

트리에서 이동을 18번하여 갈 수 있는 최대 정점의 수를 구하는 문제이다. 일반적으로 하면 13회가 나오길래 답은 14회겠구나, 생각하고 열심히 돌리다보니 14개가 나왔다. 이 트리의 센트로이드가 딱 봐도 눈에 보이는데, 그 점에서 출발하는 가장 긴 경로가 4이길래 트리의 중심에서 딱 4만큼의 이동횟수만 남기는 것을 목표로 했더니 쉽게 나왔다. 친구 말로는 이러한 형태의 모든 문제에서 트리의 지름을 지나는 데에는 1번의 이동만 사용하고, 그렇지 않은 지점을 지날 때는 2번의 이동을 사용해주면 된다고 한다.
16. 돌무더기
A에 32개의 돌, B에 33개의 돌이 있다. 나는 A-=1, A-=2, B-=1을 할 수 있고 컴퓨터는 A-=1, B-=1, B-=2를 할 수 있다. 연산을 번갈아 적용하여, A와 B가 모두 0이 되도록 만드는 사람이 이긴다. 대충 내가 A의 홀짝성을 짝수로 조절할 수 있기에, A는 홀짝성만 조절해주면서 B를 빼주는 전략을 써야겠다고 생각했다. 대충 몇 번 해보면 전략을 알겠지, 하고 슥슥 해보았더니 2번만에 이겼다. 정확한 전략은 고민해보지 않아서 모르겠다.
17. 최대공약수(12점) -12점

여기부터 약간 문제가 어지러워지기 시작했다. 일단 300번을 눌러야하는 문제가 나왔고, 유클리드 호제법을 그냥 써주면 300번 안에 문제가 풀리지 않는다. A=홀수*(2^8)이고 B=홀수*(2^7)이라는 사실을 알 수 있고, 이에 따라 A, B를 모두 홀수로 만들어준 뒤 최대공약수를 구하고 2^7을 곱해주면 된다. 여기까지는 접근을 했는데, 그 뒤로가 조금 어려워서 난 이 문제를 풀지 못했다. 최적으로 하는 방법은 기본 유클리드 호제법과 동일하게 하되, A-=B를 시행하고 짝수가 된 A를 홀수가 될때까지 나눠주는 것이라고 한다. B-=A를 적용한 이후에도 동일하다. 이를 반복하면 2XX번의 연산 끝에 최대공약수를 구할 수 있다고 한다.
18. 거짓말(13점)
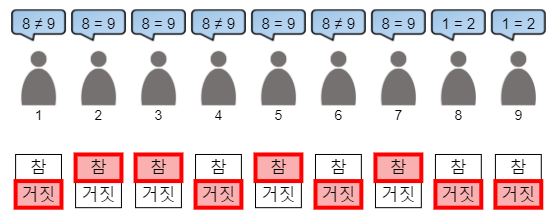
9명의 사람은 참말쟁이 또는 거짓말쟁이이다. 각 사람한테 A VS B를 물어볼 수 있으며, 이는 A와 B가 같은 유형의 사람인가? 라는 질문이다. 이때 자신에 대한 질문은 할 수 없으며, A와 B 역시 달라야한다. 9명에게 동시에 질문이 전송되며, 대답을 통해 9명 모두의 유형을 맞히면 된다.
1번부터 7번까지 8 VS 9를 물어보고, 8번과 9번에게는 1 VS 2를 물어봄으로써 해결할 수 있다. 8번과 9번에게 같은 질문을 물어봤으므로 두 사람의 대답이 같으면 8=9, 다르면 8!=9이다. 이를 통해 1~7까지의 유형을 알 수 있고, 1과 2의 유형을 알았으므로 8과 9의 유형도 알 수 있다.
배점이 높은 것치고는 매우 쉬운 문제였는데, 많은 친구들이 틀렸다. 보통 비버챌린지형 문제들은 채점이 여러 번 가능한데, 이 문제는 1번만 제출할 수 있기 때문이다. 이 조건을 보지 않고 한 번 시도해봤다가 13점을 허무하게 날린 친구들이 많다. 답이 정해져있어 질문에 대한 답을 듣게 되면 사람들의 정보를 얻는 것이므로 1번만 제출할 수 있도록 설정해놓아야 하는 것은 맞으나, 조건을 못 보고 틀린 친구들이 많아서 마음이 좀 아팠다.
19. 격자판 장식하기(15점) -15점

대각선을 원하는 방향으로 설정하고, 각 점을 동그라미, 네모, 다이아몬드 중 원하는 모양으로 바꾸어서 선분으로 이어진 두 모양은 항상 다르도록 배치하는 문제였다. 생각보다 쉽지 않았고, 많은 친구들이 틀린 것으로 안다. 나도 시험 끝나고 답을 찾았고, 답은 위와 같다.
나는 최대한 다이아몬드를 만드는 전략을 사용했다. 위의 답에 맨 마지막 줄을 제외하고 보면 나는 계속 다이아몬드 모양을 사용했는데, 이 이유는 단 하나의 모양으로도 절반 이상의 점을 커버할 수 있기 때문이었다. 이에 맞게 오른쪽을 잘 디자인해주면 문제가 어렵지 않게 풀린다. 이 문제에 시간을 조금만 더 투자하면 풀었을 것 같은데, 시간이 없어서 20번을 푸느라 못 풀었다.
20. 괄호 문자열(20점) -12점
괄호 문자열에서 swap 연산을 최소로 적용하여 주어진 구간이 모두 올바른 괄호 문자열이 되도록 하는 문제이다.



시간이 없어서 문제 1, 2, 3 밖에 못풀었고, 답은 각각 3번씩이다. 나는 첫 번째 문제를 4번을 사용하여 풀어 문제 1을 틀렸고, 문제 2와 3만 맞았다. 최적 전략은 잘 모르겠고, 열심히 노가다하다보면 답이 나오는 문제인 것 같다.
이렇게 200-7-12-15-15-12=139점을 받았다. 작년에 비해서, 그리고 나의 비버챌린지 실력에 비해서 많이 부족한 점수였다. 사실 비버챌린지는 무조건 만점을 맞고 들어간다는 생각이었는데, 생각보다 점수가 너무 안나와서 멘탈이 좀 깨졌다. 2교시에 영향을 준 것 같기도 하다.
2교시. 코딩형(300점)
총평 - 1번 2번은 실버 이하인 것 같고, 평소 실버 문제 정도는 충분히 푸는 실력인데 이 문제들을 못 풀었다면 컨디션을 원망해야할 것 같다. 3번이 조금 어려웠는데, 원래 있는 문제와 비슷하다고 하다. 게다가 특정 케이스를 고려하지 않아도 문제가 풀린다. 즉, 데이터가 약해서 문제의 정풀을 고려하지 않고도 맞은 사람이 있을 것 같다.
1. 피하자
문제 요약 : TL 2초, ML 1024MiB
배열에서 인접한 원소끼리 swap하는 연산을 최소로 하여 홀수와 짝수를 분리할 때, swap 연산의 최소 횟수를 구하는 문제이다. 배열의 길이 N<=100만이다.
문제 풀이 :
홀수의 개수를 c라 하자. 홀수를 앞으로 뺀다면 홀수들의 인덱스는 1, 2, ..., c가 될 것이다. 이러면 홀수들의 최소 이동횟수는 (원래 홀수들의 인덱스 합) - (1+2+...+c)가 될 것이고, 이를 O(N)에 계산할 수 있다. 반대로 홀수를 뒤로 뺀다면 홀수들의 인덱스는 N, N-1, ..., N-c+1이 될 것이다. 이러면 홀수들의 최소 이동횟수는 (N+(N-1)+...+(N-c+1))-(원래 홀수들의 인덱스 합)이 될 것이고, 이 역시 O(N)에 계산할 수 있다. 두 수 중에 작은 것을 출력해주면 된다.
2. ABBC
문제 요약 : TL 3초, ML 1024MiB
A, B, C로만 이루어진 문자열에서 어떤 A를 그 A보다 뒤에 있는 B와 함께 지우거나, 어떤 B를 그 B보다 뒤에 있는 C와 함께 지울 수 있다. 최대로 많이 지우고 싶을때, 지우는 횟수를 구하는 문제이다. 문자열의 길이 |S|<=30만이다.
문제 풀이 :
B는 무조건 지워지므로, B를 어떻게 지울지가 핵심이다. 우선 앞에서부터 보며 (BC)를 몇 개나 지울 수 있는지 최대 개수를 센다. 또한 뒤에서부터 보며 (AB)를 몇 개나 지울 수 있는지 최대 개수를 센다. 두 개수를 합한 것이 답이 되며, 두 개수가 합쳐서 B의 개수를 넘어간다면 B를 모두 지울 수 있다는 의미이므로 B의 개수를 출력해준다.
이 풀이가 가능한 이유가 직관적으로 이해되지 않을 수도 있는데, 우선 어떤 B에 대해서 묶어 지울 수 있는 C가 존재한다면 이 C는 그 B보다 더 앞에 있는 B와도 지워줄 수 있다. 즉, 더 앞에 있는 B는 C에 대해 더 유리한 고지에 있다. 반대로, 더 뒤에 있는 B는 A에 대해 더 유리한 고지에 있다. 따라서, 지울 수 있다면, (BC)를 지울 때는 앞에 있는 B부터 차례차례 지우고, (AB)를 지울 때는 뒤에 있는 B부터 차례차례 지워주는 것이 최적이 됨이 당연하다.
나는 1번을 푸는 데에 5분, 2번을 푸는 데에 8분이 걸렸다. 13분만에 200점은 나쁘지 않은 스타트라고 생각했고, 솔직히 여기까지는 실버 이하인 것 같다.
3. 보급
문제 요약 : TL 4초, ML 1024MiB
N개의 정점이 있고, N개의 정점의 x좌표와 y좌표는 각각 1~N 중에 하나이다. 또한 N개의 정점의 x좌표와 y좌표에는 1~N이 각각 한 번씩 나타난다. 하루에 한 정점, 총 N일 동안 N개의 정점에 보급을 줄건데, x[i]<x[j], y[i]<y[j]일 때 i번 정점은 j번 정점보다 보급을 먼저 받아야한다. 또한 각 정점은 보급을 받을 수 있는 기간이 a[i]~b[i]로 정해져있다. 이 때 N개의 정점에 모두 보급을 줄 수 있겠는가? YES면 방법도 같이 출력하고, NO면 NO라고 출력하는 문제이다.
문제 풀이 :
Dumae와 같은 문제라서 그 문제를 알고 있던 친구 2명은 문제를 각각 30분, 50분만에 풀었다고 한다. (물론 Dumae를 알고도 문제를 못푼 국대 친구 2명도 있고, Dumae를 모르고도 이 문제를 푼 친구도 봤다.) 나도 풀이를 정확히 알지는 못해 대충만 설명하자면, a와 b를 현실성 있는 범위로 압축할 수 있다. 즉, 나보다 x좌표와 y좌표가 모두 작은 정점의 a가 나의 a보다 크다면, 나의 a를 상향조정할 수 있다. 마찬가지로 b도 하향조정할 수 있는 경우가 생기고, 이에 따라 조정이 끝난 후 그리디하게 보급 일자를 주면 된다고 한다. 원본 문제에서는 간선의 개수가 10만 스케일이지만 이 문제는 간선이 최대 N^2개 존재할 수 있기에 세그 스위핑을 해야 문제를 해결할 수 있다고 한다. D5 문제인 만큼 풀이가 한 번에 이해가 가지 않아서, 나중에 Dumae를 풀어봐야겠다고 느꼈다.
처음에 내 주변 친구들이 3번을 다 풀었고, 엄청 쉬운 문제라고 하길래 완전 망한 줄 알고 기분이 안 좋았는데, 생각보다 푼 친구들이 많지 않아서 2차는 갈 수 있을 것 같다. 괜히 망한 줄 알고 답답한 마음에 화도 내고 짜증도 냈는데, 나를 옆에서 지켜보며 불편해하셨을 부모님께 죄송한 마음이 든다. 1차 때 비록 만족할만한 결과는 얻지 못했으나 2차 때 PS감을 끌어올린 상태에서 시험을 본다면 더 좋은 결과를 기대할 수 있을 것 같다.
'대회 후기' 카테고리의 다른 글
| 한국정보올림피아드(KOI 2022) 2차 시험 후기 (2) | 2022.07.17 |
|---|---|
| 한국수학올림피아드(KMO 2022) 고등부 가우스부 1차 시험 후기 (1) | 2022.05.30 |
| Codeforces Master 달성 후기 (0) | 2022.02.28 |
| Codeforces Round #767 (Div.2) (3) | 2022.01.24 |
| 2021 나코더 송년대회 후기 (3) | 2022.01.22 |